B-Tree в Go

Сегодня B-Tree обычно используется в базах данных и файловых системах для хранения и организации больших объемов данных во вторичном хранилище. Будучи структурой данных на диске, B-деревья предназначены для минимизации количества обращений к диску, необходимых для вставки, извлечения и удаления, что делает их идеальным выбором для высокоэффективных и масштабируемых систем хранения данных, обрабатывающих огромные объемы данных.

Иногда B-Tree также могут быть полезны в качестве структур данных в памяти из-за локальности ссылки при поиске. Операции поиска по B-Tree могут эффективно использовать кэширование памяти современных процессоров и в некоторых случаях даже превосходить по производительности более традиционные структуры данных в памяти, такие как красно-черные деревья или деревья AVL.

В сегодняшней статье мы рассмотрим, как работают B-Tree, реализовав в Go полнофункциональное B-Tree в памяти, обеспечивающее операции вставки, удаления и извлечения. В будущей статье мы расширим эту версию, чтобы также создать резидентное B-дерево, которое динамически сохраняет и извлекает свои узлы из вторичного хранилища. Но перед этим очень важно понять, как работает версия в памяти, поэтому давайте углубимся!

B-Tree против двоичных деревьев поиска

Давайте пробежимся по нашим знаниям о деревьях в целом.

В информатике дерево — это просто совокупность узлов, ответвляющихся от одного корневого узла. Каждый узел дополнительно содержит список ссылок на другие узлы (его дочерние узлы), а также некоторые данные с ограничением, согласно которому ни одна ссылка не может появляться в дереве более одного раза (т. е. никакие два узла не могут указывать на один и тот же узел) и не может быть никаких ссылок на корневой узел.

Например, дерево, показанное ниже, недопустимо, поскольку дочерний узел указывает на его корень, а два внутренних узла указывают на одного и того же дочернего узла:

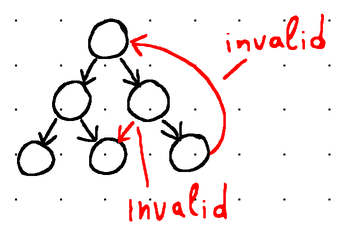
Дерево недействительно по двум причинам:

1. Листовой узел связан с корневым узлом (недопустимо).

2. Два внутренних узла связаны с одним конечным узлом (также недопустимо).

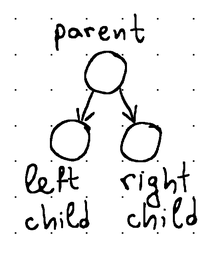
Максимальное количество дочерних узлов, которое может иметь узел, называется разветвлением. Например, бинарные деревья получили свое название от того, что у них есть разветвление, равное 2 (это означает, что каждый узел в дереве может иметь не более двух дочерних узлов, обычно называемых левым дочерним элементом и правым дочерним элементом).

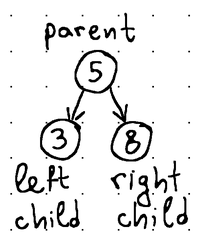
Каждый узел обычно хранит некоторый идентификатор (ключ или какое-либо значение), который можно использовать для сортировки. Мы называем дерево деревом поиска, если его узлы поддерживаются в отсортированном порядке. Например, в двоичных деревьях поиска значение левого дочернего элемента всегда меньше, а значение правого дочернего элемента больше значения родительского элемента.

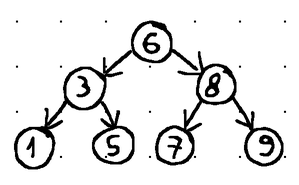
Наконец, мы можем различать сбалансированные и несбалансированные двоичные деревья поиска. Сбалансированное дерево — это, по сути, дерево, в котором высоты левого и правого поддеревьев любого узла различаются не более чем на 1 (т. е. общая высота дерева с N узлами наклоняется в сторону log2N ).

Иными словами, балансировка гарантирует, что операции вставки, удаления и извлечения могут быть выполнены за O (log n) времени (где n - общее количество узлов в дереве). Напротив, операции в несбалансированном дереве могут ухудшаться до O(n) времени (линейная временная сложность).:

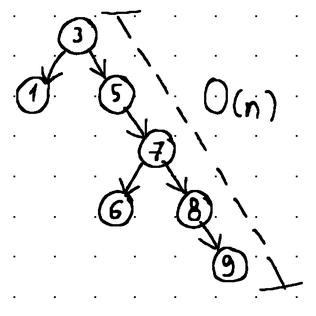
Поиск 9, удаление 9 или вставка в это дерево чего-либо большего, чем 9, потребует времени O(n).

Баланс в дереве поддерживается за счет вращений. Вращения изменяют структуру дерева, полностью переставляя связи между его узлами, сохраняя при этом их отсортированный порядок и ограничивая разницу высот между правым и левым поддеревом максимум 1.

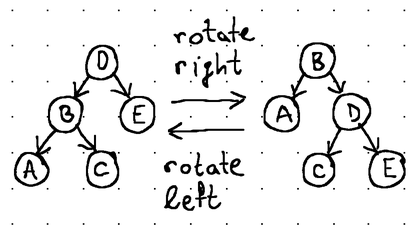
Ротации происходят по мере добавления и удаления узлов из дерева, и хотя сбалансированные двоичные деревья поиска, без сомнения, очень полезны в качестве структур данных в памяти, эти частые операции перебалансировки делают их непрактичными для использования с внешним хранилищем.

Помните, что при использовании вторичного хранилища данные передаются в основную память и из нее в единицах, называемых блоками. Таким образом, даже если мы просто хотим прочитать или записать один байт данных, по крайней мере несколько килобайт данных извлекаются из основного устройства хранения в основную память для обновления и сброса обратно на диск.

Простая вставка или удаление обычно вызывает несколько операций вращения для восстановления баланса, и иногда это может радикально изменить структуру всего дерева, а это означает, что нам часто приходится перезаписывать большие части его представления на диске (если мы хотим сохранить его во вторичном хранилище). .

Кроме того, низкое разветвление означает, что дерево обычно довольно высокое, и если предположить, что каждый узел находится в другом месте на диске из-за постоянных операций ребалансировки, обход дерева для поиска определенного значения, скорее всего, потребует от вас выполнения сканирования диска log NN. для получения данных ( количество узлов в дереве).

Теперь представьте себе оба сценария с резидентным на диске двоичным деревом поиска размером, скажем, 1 ТиБ. Необходимость сканирования 0,5 ТиБ на диске для поиска простого значения или перезаписи сотен гигабайт данных на диске только потому, что вставка изменила большую часть дерева, звучит не слишком хорошо.

Основная идея, лежащая в основе B-Tree, заключается в решении обеих этих проблем путем увеличения разветвления, тем самым уменьшая общую высоту дерева и сближая как дочерние указатели, так и элементы данных. Таким образом, тот же объем информации, который часто был бы разбросан по сотням узлов дерева бинарного поиска, теперь может храниться в одном узле B-Tree. И поскольку узел B-Tree обычно спроектирован таким образом, чтобы занимать полный блок данных во вторичном хранилище, как вставка, удаление, так и извлечение обычно могут выполняться за O(logfN) времени вместо O(log2N) времени (f - разветвление B-Tree, а N - время общее количество элементов данных в дереве).

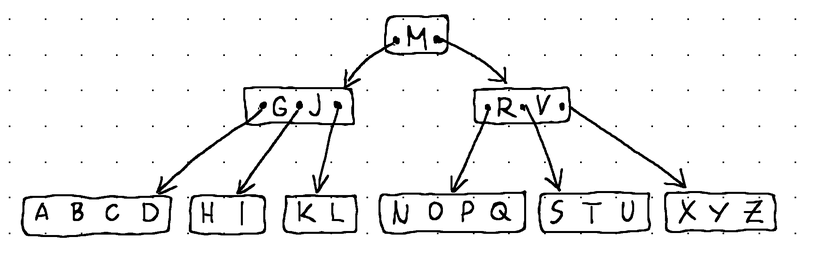
В остальном B-Tree — это просто сбалансированное дерево поиска.

Варианты B-Tree

B-Tree со временем развивалось, и сегодня существуют различные варианты, причем B+-дерево и B*-дерево, возможно, являются двумя наиболее популярными версиями. Мы очень кратко коснемся этих двух версий, чтобы противопоставить их B-Tree, которое мы собираемся реализовать в этой статье.

В традиционном B-Tree каждый узел содержит необработанные данные, а также ключи и дочерние указатели, которые можно использовать для навигации. В B+-дереве только листовые узлы содержат необработанные данные, тогда как корневой узел и внутренние узлы содержат только ключи и дочерние указатели, которые можно использовать для обхода дерева. В дополнение к этому, конечные узлы связаны друг с другом, образуя одно- или двусвязный список, используемый для упрощения последовательного сканирования всех ключей в порядке возрастания или убывания.

B*-деревья часто путают с B+-деревьями, поскольку они обладают схожими свойствами. Однако в дополнение к изменениям, присутствующим в B+деревьях, B*-деревья гарантируют, что каждый узел заполнен как минимум на 2/3 (по сравнению с 1/2 в B-деревьях и B+-деревьях), а также задерживают операции разделения на используя метод локального распределения, который пытается переместить ключи из переполненного узла в соседние узлы, прежде чем прибегать к разделению (мы обсудим операцию разделения более подробно позже в этой статье при разработке алгоритма вставки).

В сегодняшней статье мы собираемся реализовать классическое B-Tree, в котором ключи, элементы данных и дочерние указатели живут вместе в узлах дерева.

Анатомия B-Tree

B-Tree, как и любое другое дерево, состоит из узлов, и каждый узел несет в себе некоторые данные.

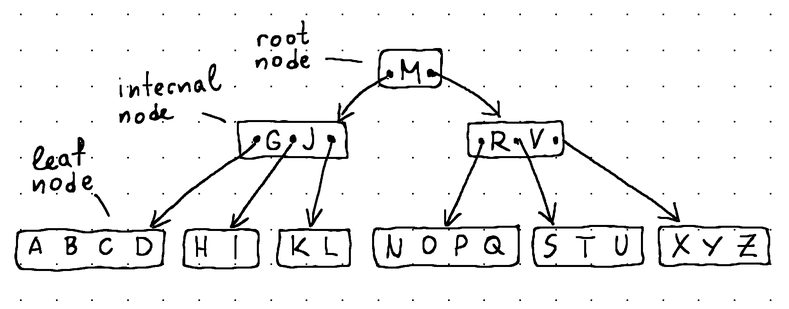
• Корневой узел находится на самом верху B-Tree и не имеет родителей.
• Листовые узлы располагаются в самом низу и не имеют детей.
• Внутренние узлы (все остальные узлы в дереве) расположены между корневым узлом и листовыми узлами и обычно охватывают несколько уровней. Они содержат как данные, так и указатели на дочерние элементы.

На все узлы накладываются некоторые ограничения, когда речь идет о количестве дочерних указателей (если они не являются конечными узлами) и количестве элементов данных, которые они могут хранить. Они не могут выйти за пределы установленного минимального и максимального порога. Эти пороги определяются степенью B-Tree.

Степень - это положительное целое число, представляющее минимальное количество дочерних элементов, на которые может указывать не-конечный узел. Например, в B-Tree со степенью d не-конечный узел может хранить не более 2d и не менее d дочерних указателей. Единственным исключением из этого правила является корневой узел, которому разрешено иметь не более двух дочерних узлов (или вообще не иметь дочерних узлов, если это лист). Минимально допустимая степень равна 2.

Кроме того, указано, что неконечный узел с N дочерними узлами всегда содержит ровно N - 1 элементов данных (по определению). Эти ограничения можно легко вывести из степени B-Tree, выполнив следующие вычисления:

const (
	degree      = 5
	maxChildren = 2 * degree       // 10
	maxItems    = maxChildren - 1  // 9
	minItems    = degree - 1       // 4
)

btree.go

Чем выше степень, тем больше узлы и, следовательно, тем больше данных мы можем поместить в один блок данных во вторичном хранилище. В системах промышленного уровня нередко можно увидеть сотни элементов данных, хранящихся в одном узле B-Tree, чтобы уменьшить дисковый ввод-вывод.

Реализация B-Tree

Выполнив degree приведенные выше вычисления, мы начали закладывать основу для нашей реализации B-Tree. Продолжим и определим основные необходимые для этого структуры.

Как мы объясняли, дерево состоит из узлов, а узлы содержат элементы данных. Предположим, что каждый элемент может содержать в качестве данных любую произвольную последовательность байтов. В дополнение к этому нам понадобится некоторая форма ключа для уникальной идентификации каждого элемента данных и поддержания порядка сортировки в нашем дереве.

Поэтому мы можем использовать следующую структуру для представления наших элементов данных:

type item struct {
	key []byte
	val []byte
}

узел.go

Из degree мы знаем, что узел может содержать максимум maxItems элементов и maxChildren дочерних элементов. При проектировании нашей nodeструктуры мы можем использовать это для указания двух массивов с фиксированной емкостью, называемых items и children. items будет содержать все элементы данных, хранящиеся в узле, а также childrenуказатели на дочерние узлы.

Мы используем массивы фиксированного размера вместо срезов, чтобы избежать дорогостоящих операций расширения срезов во время последующей вставки. Фиксированный размер также облегчит нам хранение представления B-Tree на диске (если мы решим сделать это впоследствии).

Для отслеживания занятых слотов в каждом из вышеупомянутых массивов мы также определяем два счетчика с именами numItems и numChildren. По numChildren счетчику мы можем сделать вывод, является ли узел листовым узлом или нет, что нам пригодится, когда мы начнем реализовывать вставку и удаление позже. Имея это в виду, мы также определяем isLeaf() метод, позволяющий различать внутренние узлы и листовые узлы.

Код гласит:

type node struct {
	items       [maxItems]*item
	children    [maxChildren]*node
	numItems    int
	numChildren int
}

func (n *node) isLeaf() bool {
	return n.numChildren == 0
}

В заключение этого раздела мы определим нашу основную структуру B-Tree и определим простой метод, который инкапсулирует ее инициализацию. По сути, структура B-Tree хранит только указатель на корневой узел дерева:

type BTree struct {
	root *node
}

func NewBTree() *BTree {
	return &BTree{}
}

Поиск в B-Tree

Прежде чем мы сможем выполнить поиск по всему дереву, нам необходимо реализовать поиск узлов. Поиск узла — это процесс поиска конкретного узла по определенному ключу. Поиск узлов также необходим для последующей реализации вставки и удаления.

Поскольку для узлов B-Tree типично содержать сотни элементов данных, выполнение линейного поиска было бы весьма неэффективным, поэтому большинство реализаций B-Tree вместо этого полагаются на двоичный поиск.

Если использовать нашу внутреннюю node структуру, простой алгоритм двоичного поиска будет выглядеть так:

func (n *node) search(key []byte) (int, bool) {
	low, high := 0, n.numItems
	var mid int
	for low < high {
		mid = (low + high) / 2
		cmp := bytes.Compare(key, n.items[mid].key)
		switch {
		case cmp > 0:
			low = mid + 1
		case cmp < 0:
			high = mid
		case cmp == 0:
			return mid, true
		}
	}
	return low, false
}

Здесь, если элемент данных, соответствующий указанному ключу, присутствует в текущем узле, search() метод возвращает его точную позицию. В противном случае метод возвращает позицию, в которой находился бы элемент с этим ключом, если бы он присутствовал в узле. Дополнительным преимуществом для нелистовых узлов является то, что эта позиция соответствует позиции дочернего узла, где может существовать ключ с этим значением.

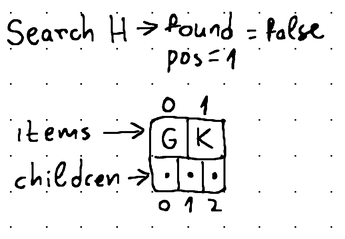
Если бы «H» присутствовал в этом узле, он находился бы в позиции 1 (а «K» находился бы в позиции 2). Более того, элемент с этим ключом все еще может присутствовать в дочернем элементе с индексом 1.

Во всех случаях search() метод также возвращает логическое значение, указывающее, успешен поиск или нет.

Это делает обход довольно простым, поскольку если логическое значение равно false, мы можем использовать возвращенную позицию для продолжения обхода дерева, пока в конечном итоге не найдем элемент данных с нужным ключом.

Следовательно, мы можем выполнить поиск по всему дереву следующим образом:

func (t *BTree) Find(key []byte) ([]byte, error) {
	for next := t.root; next != nil; {
		pos, found := next.search(key)

		if found {
			return next.items[pos].val, nil
		}

		next = next.children[pos]
	}

	return nil, errors.New("key not found")
}

Вставка данных

Вставка данных предполагает обход дерева до тех пор, пока мы не найдем листовой узел, способный разместить наш элемент данных, сохраняя при этом отсортированный порядок по всему дереву и сохраняя элементы в границах, установленных minItems и maxItems.

Начнем с определения вспомогательного метода, который позволяет нам вставлять элемент данных в любую произвольную позицию узла B-Tree:

func (n *node) insertItemAt(pos int, i *item) {
	if pos < n.numItems {
		// Make space for insertion if we are not appending to the very end of the "items" array
		copy(n.items[pos+1:n.numItems+1], n.items[pos:n.numItems])
	}
	n.items[pos] = i
	n.numItems++
}

Естественно, достижение конечного узла не гарантирует, что узел имеет достаточную емкость для размещения нашего элемента данных. Возможно, он уже заполнен. В таких случаях мы выполняем преобразование, называемое «разделение узла»:

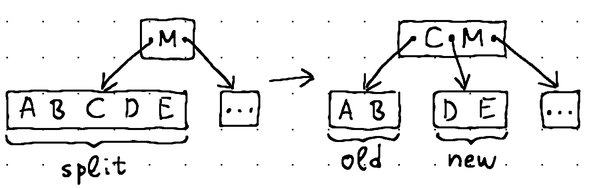
Узел, содержащий элементы [A, B, C, D, E], разделяется на два узла, содержащие элементы [A, B] и [D, E]. Узел [D, E] — это вновь созданный узел. Средний элемент [C] перемещается в родительский узел.

При разделении узла мы вводим в дерево совершенно новый узел. Мы извлекаем средний элемент из существующего листового узла и перемещаем его к родительскому узлу. Затем мы берем вторую половину элементов данных из существующего листового узла и перемещаем их во вновь созданный узел. Наконец, мы связываем вновь созданный узел с родительским, вставляя новый указатель на дочерний элемент сразу после среднего элемента.

Необходимость перестановки дочерних элементов требует добавления в нашу node структуру еще одного вспомогательного метода:

func (n *node) insertChildAt(pos int, c *node) {
	if pos < n.numChildren {
		// Make space for insertion if we are not appending to the very end of the "children" array.
		copy(n.children[pos+1:n.numChildren+1], n.children[pos:n.numChildren])
	}
	n.children[pos] = c
	n.numChildren++
}

Разделение листового узла предполагает, что его родительский узел имеет достаточную емкость для размещения среднего элемента. Однако родительский элемент также легко может быть полным, и мы можем столкнуться с той же ситуацией с его предками. По этой причине разделение узлов нередко распространяется вплоть до корня дерева. Это требует тщательного рассмотрения при планировании реализации метода split().

Что мы можем сделать, так это заставить наш код вставки рекурсивно обходить дерево, гарантируя, что каждый последующий узел на пути к нашему листу имеет достаточную емкость для размещения нового элемента (помните, что разделение узлов может распространяться до корня).

Это означает, что мы можем выполнить разделение, как только достигнем родителя дочернего элемента, который уже заполнен. Наш split() метод создаст новый узел и переместит все необходимые элементы данных и дочерние указатели из существующего дочернего узла в новый узел. Он также вернет средний элемент из существующего дочернего узла, чтобы мы могли переместить его в родительский узел.

Вот весь код для выполнения разделения:

func (n *node) split() (*item, *node) {
	// Retrieve the middle item.
	mid := minItems
	midItem := n.items[mid]

	// Create a new node and copy half of the items from the current node to the new node.
	newNode := &node{}
	copy(newNode.items[:], n.items[mid+1:])
	newNode.numItems = minItems

	// If necessary, copy half of the child pointers from the current node to the new node.
	if !n.isLeaf() {
		copy(newNode.children[:], n.children[mid+1:])
		newNode.numChildren = minItems + 1
	}

	// Remove data items and child pointers from the current node that were moved to the new node.
	for i, l := mid, n.numItems; i < l; i++ {
		n.items[i] = nil
		n.numItems--

		if !n.isLeaf() {
			n.children[i+1] = nil
			n.numChildren--
		}
	}

	// Return the middle item and the newly created node, so we can link them to the parent.
	return midItem, newNode
}

Вы наверняка заметили, что в приведенном выше коде мы также иногда перемещаем дочерние указатели. Это связано с тем, что операция разделения может распространяться до корня, и в этом случае мы будем разбивать нелистовые узлы. Разделение нелистовых узлов не является чем-то необычным. В таких случаях нам просто нужно переместить половину дочерних указателей из разбивающегося дочернего узла во вновь созданный узел.

Полный код для вставки нового элемента в дерево выглядит следующим образом:

func (n *node) insert(item *item) bool {
	pos, found := n.search(item.key)

	// The data item already exists, so just update its value.
	if found {
		n.items[pos] = item
		return false
	}

	// We have reached a leaf node with sufficient capacity to accommodate insertion, so insert the new data item.
	if n.isLeaf() {
		n.insertItemAt(pos, item)
		return true
	}

	// If the next node along the path of traversal is already full, split it.
	if n.children[pos].numItems >= maxItems {
		midItem, newNode := n.children[pos].split()
		n.insertItemAt(pos, midItem)
		n.insertChildAt(pos+1, newNode)
		// We may need to change our direction after promoting the middle item to the parent, depending on its key.
		switch cmp := bytes.Compare(item.key, n.items[pos].key); {
		case cmp < 0:
			// The key we are looking for is still smaller than the key of the middle item that we took from the child,
			// so we can continue following the same direction.
		case cmp > 0:
			// The middle item that we took from the child has a key that is smaller than the one we are looking for,
			// so we need to change our direction.
			pos++
		default:
			// The middle item that we took from the child is the item we are searching for, so just update its value.
			n.items[pos] = item
			return true
		}

	}

	return n.children[pos].insert(item)
}

Как видите, код ожидает, что узел будет служить его отправной точкой. По логике, этот узел должен быть корнем дерева (т.е. мы должны начать вставку вызовом tree.root.insert(item)). Затем алгоритм начнет обход дерева от его корня, рекурсивно вызывая insert() метод, пока не достигнет листового узла, подходящего для вставки. Если элемент данных с данным ключом уже существует в дереве, мы можем просто обновить его значение, а не создавать новый элемент.

Мы инкапсулируем первоначальный tree.root.insert(item)вызов в отдельный метод, который будет частью нашей структуры B-Tree. Но прежде чем мы доберемся до этого, стоит объяснить, что нужно сделать, если сам корневой узел уже заполнен.

Разделение корневого узла немного отличается от разделения других узлов. Когда корневой узел заполнен, нет родительского элемента, к которому можно было бы переместить средний элемент, и нет места для введения нового родственного узла. Таким образом, в случае корневых узлов операция разделения включает в себя введение совершенно нового корневого узла для замены существующего корня. Существующий корень затем становится левым дочерним элементом нового корня. Одновременно мы вводим еще один новый узел, который будет играть роль правого дочернего элемента нового корня. Половина элементов из существующего корня перемещается в новый правый дочерний элемент, а средний элемент становится единственным элементом данных во вновь введенном корневом узле.

Код гласит:

func (t *BTree) splitRoot() {
	newRoot := &node{}
	midItem, newNode := t.root.split()
	newRoot.insertItemAt(0, midItem)
	newRoot.insertChildAt(0, t.root)
	newRoot.insertChildAt(1, newNode)
	t.root = newRoot
}

На этом мы можем завершить этот раздел, добавив метод-оболочку в нашу структуру B-Tree, чтобы облегчить вставку:

func (t *BTree) Insert(key, val []byte) {
	i := &item{key, val}

	// The tree is empty, so initialize a new node.
	if t.root == nil {
		t.root = &node{}
	}

	// The tree root is full, so perform a split on the root.
	if t.root.numItems >= maxItems {
		t.splitRoot()
	}
	
	// Begin insertion.
	t.root.insert(i)
}

Наше B-Tree теперь готово для хранения данных.

Удаление данных

По сравнению со вставкой удаление требует немного больше усилий для реализации, поскольку для поддержания сбалансированности дерева может потребоваться гораздо больше потенциальных преобразований.

Давайте начнем с добавления в нашу node структуру еще одного вспомогательного метода, который позволит нам удалить элемент данных из любой заданной позиции в itemsмассиве. Для удобства мы также вернем удаленный товар. Это пригодится позже, при реализации окончательного алгоритма удаления.

func (n *node) removeItemAt(pos int) *item {
	removedItem := n.items[pos]
	n.items[pos] = nil
	// Fill the gap, if the position we are removing from is not the very last occupied position in the "items" array.
	if lastPos := n.numItems - 1; pos < lastPos {
		copy(n.items[pos:lastPos], n.items[pos+1:lastPos+1])
		n.items[lastPos] = nil
	}
	n.numItems--

	return removedItem
}

При удалении элемента есть две возможности: он может находиться на внутреннем узле или на листовом узле. Для конечных узлов мы можем просто удалить элемент. Однако при использовании внутренних узлов мы должны сначала найти неупорядоченного преемника элемента, поменять его местами с исходным элементом, а затем извлечь неупорядоченного преемника из листового узла, где мы его нашли.

В обоих случаях удаление элемента может привести к опустошению конечного узла. Недополнение — это состояние, при котором узел содержит меньше элементов, чем предел, объявленный параметром minItems.

Недополнение можно устранить путем слияния узла с его соседом или заимствования элементов у соседних узлов. В совокупности мы называем эту операцию «заполнением узла» (поскольку мы так или иначе заполняем узел элементами, чтобы восстановить пределы, установленные minItems).

Хотя операции заимствования обычно не нарушают баланс дерева, операции слияния «крадут» элементы из родительских узлов и, следовательно, могут привести к дальнейшему уменьшению переполнения, распространяющемуся до корня дерева. Это важно учитывать при разработке алгоритма удаления.

В свете этого факта во время слияния нам наверняка придется реорганизовать дочерние узлы, поэтому давайте добавим в нашу node структуру еще один вспомогательный метод, чтобы упростить нашу реализацию:

func (n *node) removeChildAt(pos int) *node {
	removedChild := n.children[pos]
	n.children[pos] = nil
	// Fill the gap, if the position we are removing from is not the very last occupied position in the "children" array.
	if lastPos := n.numChildren - 1; pos < lastPos {
		copy(n.children[pos:lastPos], n.children[pos+1:lastPos+1])
		n.children[lastPos] = nil
	}
	n.numChildren--

	return removedChild
}

Вот как на практике выглядят различные операции заполнения:

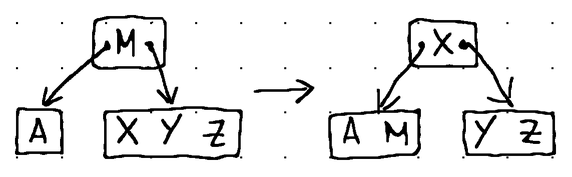
В узле [A] происходит опустошение. Поэтому мы заимствуем первый элемент у его соседнего справа брата [X, Y, Z]. Элемент [X] перемещается вверх в родительский узел, чтобы заменить элемент [M], который перемещается в нижний узел.

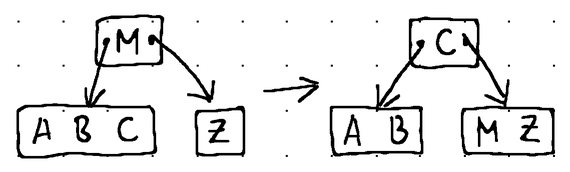
В узле [Z] происходит опустошение. Поэтому мы заимствуем последний элемент у его соседнего слева брата [A, B, C]. Элемент [C] перемещается вверх в родительский узел, чтобы заменить элемент [M], который перемещается в нижний узел.

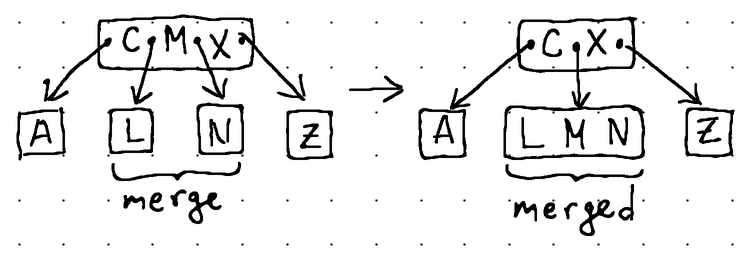Элемент [M] забирается у родительского элемента [C, M, X] и перемещается в левого родственного элемента [L]. После этого все элементы из правого брата [N] также перемещаются в левого брата. Наконец, правый узел и его указатель отбрасываются, и восстановленный узел становится [L, M, N].

В терминах кода Go операции заимствования и слияния можно выразить следующим образом:

func (n *node) fillChildAt(pos int) {
	switch {
	// Borrow the right-most item from the left sibling if the left
	// sibling exists and has more than the minimum number of items.
	case pos > 0 && n.children[pos-1].numItems > minItems:
		// Establish our left and right nodes.
		left, right := n.children[pos-1], n.children[pos]
		// Take the item from the parent and place it at the left-most position of the right node.
		copy(right.items[1:right.numItems+1], right.items[:right.numItems])
		right.items[0] = n.items[pos-1]
		right.numItems++
		// For non-leaf nodes, make the right-most child of the left node the new left-most child of the right node.
		if !right.isLeaf() {
			right.insertChildAt(0, left.removeChildAt(left.numChildren-1))
		}
		// Borrow the right-most item from the left node to replace the parent item.
		n.items[pos-1] = left.removeItemAt(left.numItems - 1)
	// Borrow the left-most item from the right sibling if the right
	// sibling exists and has more than the minimum number of items.
	case pos < n.numChildren-1 && n.children[pos+1].numItems > minItems:
		// Establish our left and right nodes.
		left, right := n.children[pos], n.children[pos+1]
		// Take the item from the parent and place it at the right-most position of the left node.
		left.items[left.numItems] = n.items[pos]
		left.numItems++
		// For non-leaf nodes, make the left-most child of the right node the new right-most child of the left node.
		if !left.isLeaf() {
			left.insertChildAt(left.numChildren, right.removeChildAt(0))
		}
		// Borrow the left-most item from the right node to replace the parent item.
		n.items[pos] = right.removeItemAt(0)
	// There are no suitable nodes to borrow items from, so perform a merge.
	default:
		// If we are at the right-most child pointer, merge the node with its left sibling.
		// In all other cases, we prefer to merge the node with its right sibling for simplicity.
		if pos >= n.numItems {
			pos = n.numItems - 1
		}
		// Establish our left and right nodes.
		left, right := n.children[pos], n.children[pos+1]
		// Borrow an item from the parent node and place it at the right-most available position of the left node.
		left.items[left.numItems] = n.removeItemAt(pos)
		left.numItems++
		// Migrate all items from the right node to the left node.
		copy(left.items[left.numItems:], right.items[:right.numItems])
		left.numItems += right.numItems
		// For non-leaf nodes, migrate all applicable children from the right node to the left node.
		if !left.isLeaf() {
			copy(left.children[left.numChildren:], right.children[:right.numChildren])
			left.numChildren += right.numChildren
		}
		// Remove the child pointer from the parent to the right node and discard the right node.
		n.removeChildAt(pos + 1)
		right = nil
	}
}

Метод fillChildAt() кажется огромным, но если вы внимательно прочитаете комментарии, вы сможете получить четкое представление о том, как работают различные типы операций заполнения.

Для фактического удаления мы рекурсивно проходим по дереву, начиная с его корня, в поисках элемента данных, соответствующего ключу, который мы хотим удалить. Мы можем найти ключ, находящийся либо во внутреннем узле, либо в листовом узле. Для конечных узлов мы можем просто удалить элемент. Однако для внутренних узлов нам необходимо изменить путь обхода, чтобы найти неупорядоченного преемника (неупорядоченный преемник — это элемент, имеющий наименьший ключ в правом поддереве, который больше, чем ключ текущего элемента).

Когда мы находим неупорядоченного преемника, мы удаляем его из листового узла, в котором он находится, а затем возвращаем его предыдущему вызову в стеке вызовов, чтобы его можно было использовать для замены исходного элемента данных, который мы намеревались удалить.

Обходя дерево обратно от листа к корню, мы проверяем, не вызвали ли мы потерю памяти при нашем удалении или любых последующих слияниях, и выполняем соответствующее исправление.

Код выглядит следующим образом:

func (n *node) delete(key []byte, isSeekingSuccessor bool) *item {
	pos, found := n.search(key)

	var next *node

	// We have found a node holding an item matching the supplied key.
	if found {
		// This is a leaf node, so we can simply remove the item.
		if n.isLeaf() {
			return n.removeItemAt(pos)
		}
		// This is not a leaf node, so we have to find the inorder successor.
		next, isSeekingSuccessor = n.children[pos+1], true
	} else {
		next = n.children[pos]
	}

	// We have reached the leaf node containing the inorder successor, so remove the successor from the leaf.
	if n.isLeaf() && isSeekingSuccessor {
		return n.removeItemAt(0)
	}

	// We were unable to find an item matching the given key. Don't do anything.
	if next == nil {
		return nil
	}

	// Continue traversing the tree to find an item matching the supplied key.
	deletedItem := next.delete(key, isSeekingSuccessor)

	// We found the inorder successor, and we are now back at the internal node containing the item
	// matching the supplied key. Therefore, we replace the item with its inorder successor, effectively
	// deleting the item from the tree.
	if found && isSeekingSuccessor {
		n.items[pos] = deletedItem
	}

	// Check if an underflow occurred after we deleted an item down the tree.
	if next.numItems < minItems {
		// Repair the underflow.
		if found && isSeekingSuccessor {
			n.fillChildAt(pos + 1)
		} else {
			n.fillChildAt(pos)
		}
	}

	// Propagate the deleted item back to the previous stack frame.
	return deletedItem
}

Подобно вставке, мы извлекаем отправную точку нашего алгоритма удаления в метод, прикрепленный непосредственно к структуре B-Tree, который выглядит следующим образом:

func (t *BTree) Delete(key []byte) bool {
	if t.root == nil {
		return false
	}
	deletedItem := t.root.delete(key, false)

	if t.root.numItems == 0 {
		if t.root.isLeaf() {
			t.root = nil
		} else {
			t.root = t.root.children[0]
		}
	}

	if deletedItem != nil {
		return true
	}
	return false
}

Теперь у нас есть полностью работающая процедура удаления.

Заключение

На этом мы завершаем нашу статью о B-Tree (B-деревьях). Спасибо за прочтение.